Questões
1
Se m e n são inteiros primos entre si, então o máximo divisor comum entre m+n e m-n:
(A) é sempre 1.
(B) é sempre 2.
(C) é sempre 3.
(D) só pode ser 1 ou 2.
(E) pode ser qualquer inteiro.
2 Sejam R e S as regiões do plano delimitadas pelos círculos de equações x2 + y2 = 1 e (x-1)2 + y2 = 1, respectivamente. A área de R Ç S é:

3 Se
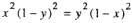 e
e 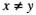 então
então
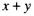 será:
será:

4 Se, em um encontro de n pessoas, todas apertarem as mãos entre si, então o número de apertos de mão será:

5 A probabilidade de duas pessoas fazerem aniversário no mesmo dia é:
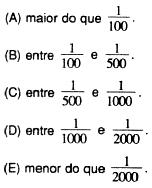
6 Consideremos o círculo C de raio r e um quadrado Q circunscrito a C. A área interior a Q e exterior a C se subdivide em quatro áreas idênticas, cada uma valendo:
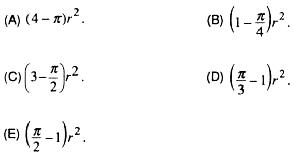
7 A equação tan(x)=cos(x) tem, para x no intervalo
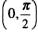 , uma raiz x =
, uma raiz x = 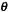 q sobre a qual podemos dizer:
q sobre a qual podemos dizer:
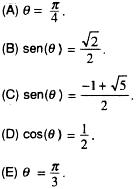
8
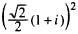 =
=
(A) 1.
(B) -1.
(C) i.
(D) -i.
(E) 0.
9 Um polígono regular de n lados tem 90 diagonais. O valor de n é:
(A) 10.
(B) 12.
(C) 15.
(D) 20.
(E) 21.
10 Para
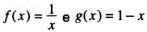 temos que
temos que 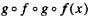 é
é
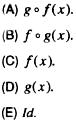
11 O coeficiente de x na expansão de
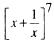 é:
é:
(A)0. (B) 7. (C) 28. (D) 35. (E) 49.
12 Uma prova de múltipla escolha tem 10 questões, com três respostas em cada questão. Um aluno que nada sabe da matéria vai responder a todas as questões ao acaso, e a probabilidade que ele tem de não tirar zero é:
(A) maior do que 96%.
(B) entre 94% e 96%.
(C) entre 92% e 94%.
(D) entre 90% e 92%.
(E) menor do que 90%.
13 Dado um polígono regular de 11 lados, se unirmos seu centro a cada um de seus vértices, obteremos 11 triângulos isósceles iguais, cada um dos quais tendo dois ângulos internos iguais a:

14 Foram enviadas quatro cartas para endereços diferentes, e, na hora de colocar cada uma no respectivo envelope, trocaram-se inadvertidamente as cartas. Qual a probabilidade de que nenhuma carta tenha afinal sido enviada para o endereço certo?
(A) 3/8. (B) 1/4.
(C) 31/12. (D) 7/24.
(E) 5/12.
15 Considere o triângulo ABC em que AB=BC=1. Seja D o ponto médio de AC, e E o ponto médio de AB. O comprimento de DE vale:
 Respostas: 1) D, 2) , 3) D, 4) C, 5) B, 6) B, 7) C, 8)C
Respostas: 1) D, 2) , 3) D, 4) C, 5) B, 6) B, 7) C, 8)C9) C, 10) B, 11) D, 12) A, 13) E, 14) A, 15) D

Nenhum comentário:
Postar um comentário